WebGL でマンデルブロ集合とジュリア集合
複素平面を理解する
普段使う”数”に実数 (real number) がある。例えば 0, 1, -10, 0.3, 1/2, √2 など。
これとは別に、虚数 (imaginary number) がある。虚数は √-1 や √(-1/2) などといった、2 乗すると 0 未満になる数のこと。
実数と虚数は、直接足したり掛けたりすることはできない。水と油のような関係。実数の単位は 1 に対して、一般的に虚数の単位は i とする。
実数と虚数を混ぜた数は 10 1 + 10 i のようになる。実数と虚数が混ざった数を複素数 (complex number) という。
複素数は、実数と虚数を軸に、2 次元の平面で表すことができる。これを複素平面 (complex plane) という。例えば、複素数 3 + 2i は次の青い点のように表すことができる。
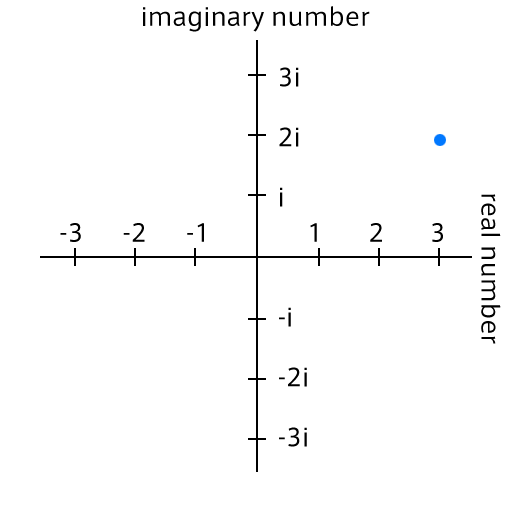
漸化式と発散
マンデルブロ集合は、漸化式
Zn+1 = Zn2 + C
ただし、Z0 = 0
を複素平面上の全ての複素数 (座標) C に対して行い、漸化式にあてはめ再起的に処理すると
- 確定せず振動する場合
- 無限となり発散する場合
に分かれる。発散しない場合の C 全体をマンデルブロ集合といい、その全ての座標に色をつけると独特のあの形状となる。
例えば、C = -1 1 + 0 i、つまり -1、複素平面上の ( -1, 0 ) を上記の漸化式に当てはめると…

の様に同じあたいを行き来し発散しない。つまり、-1 はマンデルブロ集合に属すことになる。なので、座標 ( -1, 0 ) を塗りつぶす。
一方で、C = -1 1 + 1 i つまり -1 + i、複素平面上の ( -1, 1 ) では

の様に、最終的に無限となり発散する。 -1 + i はマンデルブロ集合に属さない。なので、座標 ( -1, i ) は塗りつぶさない
このように全ての複素平面上の座標に対して、同じことを繰り返すわけだ。
なお、C の絶対値が 2 以上のときは必ず発散するので絶対にマンデルブロ集合に属さない。
GLSL で描く
フラグメントシェーダーでの gl_FragCoord を加工して複素平面の座標として使い、複素数を vec2 形式で代用する。uniform resolution は、ビューポート (canvas要素) の縦横の大きさをピクセル単位で入力している。

#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 resolution;
const int ITETARION = 300; // 振動 or 発散を判断する上限
void main( void ) {
vec2 position = ( ( gl_FragCoord.xy / resolution.xy ) * 2. - 1. ) * resolution / resolution.y;
vec2 z = vec2( 0, 0 ); // Zn (xは実部、yは虚部)
vec2 zNext = vec2( 0, 0 ); // Zn+1 (xは実部、yは虚部)
vec2 c = position.xy; // 複素平面上の座標 (xは実部、yは虚部)
bool diverge = false; // 発散する true, しない false。発散しないならマンデルブローセット。
int elapsed = 0;
for ( int i = 0; i < ITETARION; i ++ ) {
zNext.x = pow( z.x, 2. ) - pow( z.y, 2. );
zNext.y = 2. * z.x * z.y ;
z = zNext + c;
if ( length( z ) > 2. ) {
diverge = true;
break;
}
elapsed = i;
}
if( diverge ) {
gl_FragColor = vec4( 1 );
} else {
gl_FragColor = vec4( 0, 0, 0, 1 );
}
}
色をつけてみる。mod を用いて、発散するまでに要した繰り返し回数の “あまり” に応じて色を変える
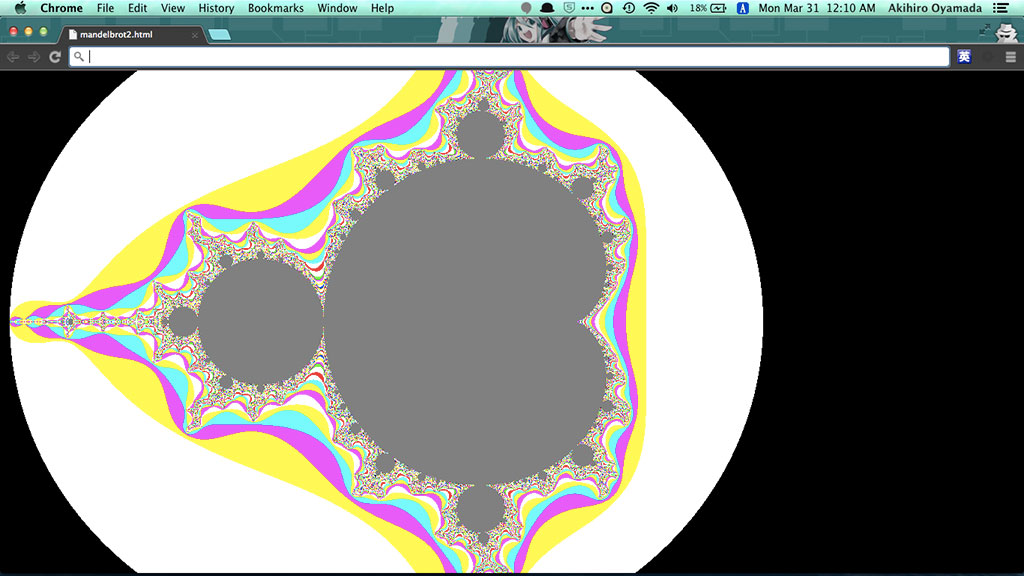
uniform で経過時間を入力し、sin( 経過時間 ) に応じて拡大させると、フラクタルを実感できる。最大拡大時に、形状が劣化している部分は、発散を判断するまでの再起回数が十分でないため。for の繰り返し処理の無限回に近づけることでより鮮明にできる。
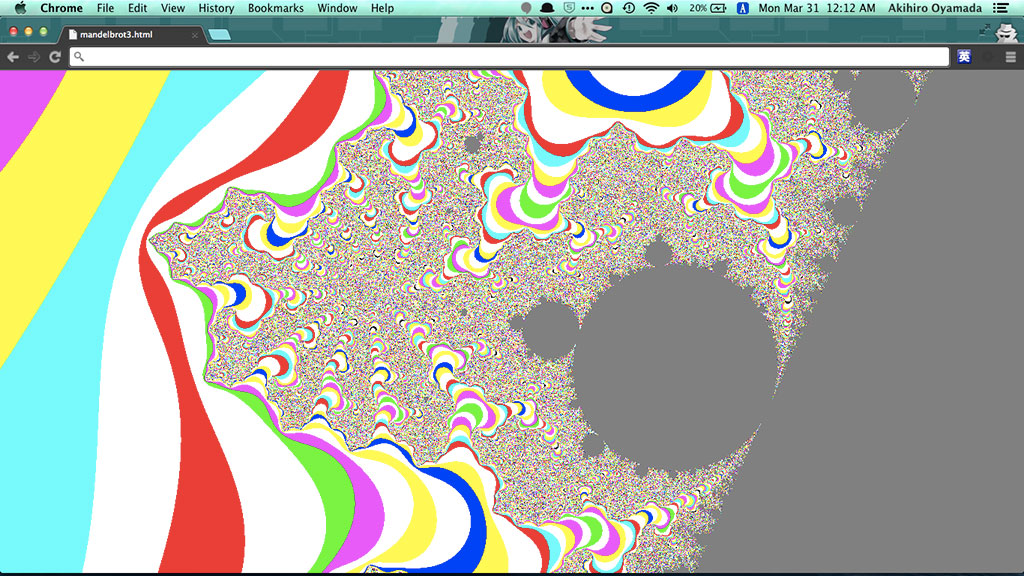
ジュリア集合
マンデルブロの漸化式
Zn+1 = Zn2 + C
の C を任意の複素数に固定し、Z0を平面の座標として使い、発散を判断すればジュリア集合となる。
次の例では、C を 0.5 + 0.5i で固定している。マンデルブロセットで描かれる図形のように自己相似な図形が繰り返されており美しい。
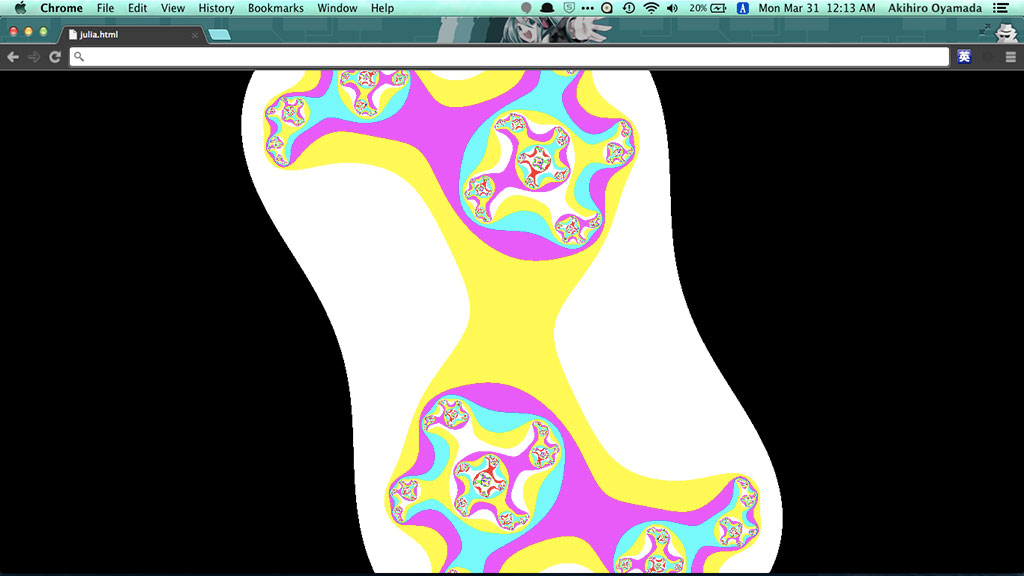
複素数 C を時間に応じて変化させると面白いアニメーションとなる。
参考