自然の中の数学、ボロノイ Math in Nature, Voronoi

任意の点群からドロネー図 ( Delaunay diagram ) とそこからボロノイ図 ( Voronoi diagram ) を作るクラスを書いてみました。

I have written a class which makes Delaunay diagrams and Voronoi diagrams in JavaScript.

ドロネー図の考え方は ProcessingでDelaunay分割（解説篇）や @edo_m18 さんの Qiita 投稿 がとても参考になりました。

ドロネー図は、点3つからなる三角形の外接円内に、他の点を含まない三角形の集合です。一方、ボロノイ図は、ドロネー図で得た三角形の外接円の中心を結んだ、多角形の集合です。

Check this links to understand the algorithm: ProcessingでDelaunay分割（解説篇） and a post on Qiita by @edo_m18

The Delaunay diagrams consist of triangles which don’t contain any other point in its circumcircle, and the Voronoi diagram consists of polygons which can be made from the center of the circumcircle of the Delaunay triangles.

• ドロネー図の例, an example of Delaunay
• ボロノイ図の例, an example of Voronoi

ボロノイ図は、母点からの縄張りが形になって現れます。なんだか有機的に見えますね。

The Voronoi diagram shows the territories of each point. It looks like something organic, doesn’t it?

実は、自然の中には、たくさんのボロノイ図に似た模様が存在します。キリンや、トンボの羽がボロノイに近いのは知っている人もいるかもしれませんね。

Actually, there are many Voronoi like patterns in Nature. You might know that the Giraffe skin and Dragonfly wings look like Voronoi patterns.

ウミガメの頭や足

Sea turtle’s head and arms

細胞の並び

Also this plant cells

とうもろこしの粒

And corn

フラクタルなどもそうですが、自然の中に隠れている数学的な模様は美しいですし、おもしろいですよね。

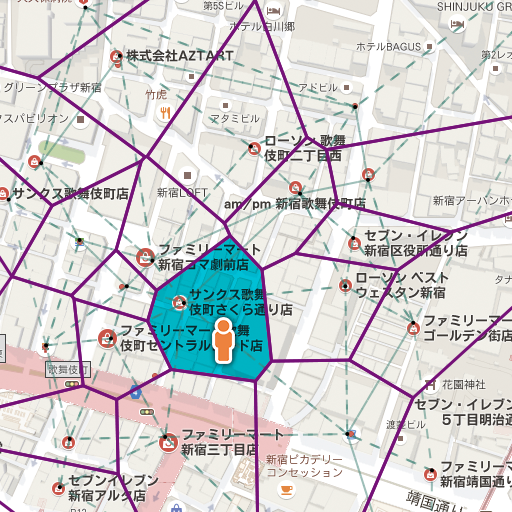
他にも、ボロノイ図を使うと、例えば、現在位置から一番近いコンビニの場所を知ることもできます。この図からは各コンビニの守備範囲も読み取れますね。

Along with Voronoi patterns, patterns which are hidden in Nature are beautiful and interesting, such as Fractal patterns.

Another feature of Voronoi is its ability to find the closest point, for example convenient stores. You can also see the area that each store covers.

ボロノイエディターを作ってみたので、いろいろ展をうってみるとおもしろいかと思います。（最外周の部分は不完全ですが…）

I have also made a Voronoi Editor. It may be interesting for you.

ちなみに、キリンの模様は実際には反応拡散系という、シマウマやヒョウと同じ仕組みで描くことができるようなので、次はそれを試してみようと思います。